Let
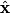 be the direction of the incoming photon, and let be the direction of the incoming photon, and let 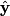 be the direction of the outgoing photon. Let be the direction of the outgoing photon. Let 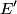 be the energy of the photon after it is scattered and let be the energy of the photon after it is scattered and let 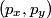 be the momentum of the electron after the the photon scatters off of it. Conservation of energy and momentum gives be the momentum of the electron after the the photon scatters off of it. Conservation of energy and momentum gives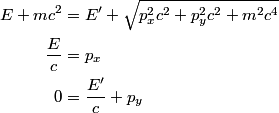 Plugging the second and third equations into the first equation gives 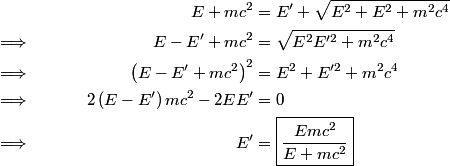 Therefore, answer (E) is correct. |